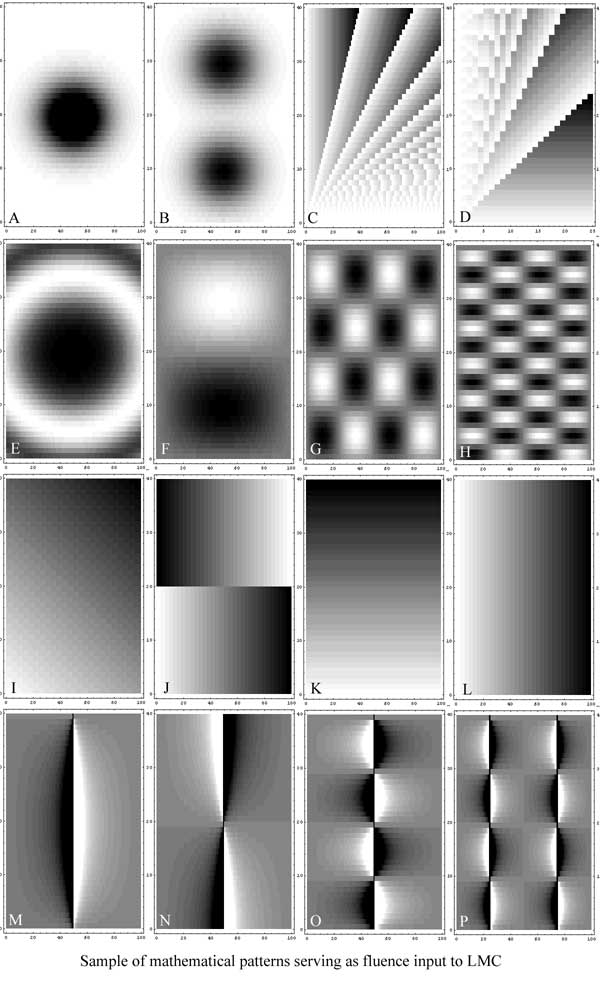
The following 16 test
patterns (A to P) are generated with mathematical formulas (1 to 16).
They serve as input to the LMC and give a 25 by 40cm radiation field. The
fluence resolution in cross plane direction is 2.5mm, inplane it is 1cm (the
leaf width at isocenter).
Guess the right combination of pattern and formula and send an email with
your address to:
harald.krauss [at] wienkav.at
You have the chance to win a set of six "Absolut MLC" Art-cards!
First the patterns:
Now the formulas:
First some explanations: h=40 is the height of the field (40cm), w=100 is the field width times 4 (since each fluence pixel is 2.5mm wide). The parameter a denotes the aspect ratio which is used to plot the pattern in Mathematica with the right proportions and is defined as 4*h/w.
For Mathematica users: the pattern is then plotted with the command "ListDensityPlot[-pattern, AspectRatio -> a, ImageSize -> 300, Mesh -> False]".
Formula 1: pattern = Table[N[(1 + Sin[ 12 Pi 1 y/h]*Sin[ 4 Pi 1x/w])/2], {y, h}, {x, w}]
Formula 2: pattern = Table[N[(1 + Sin[ 2 Pi 2 y/h]*Sin[ 2 Pi 2x/w])/2], {y, h}, {x, w}]
Formula 3: pattern = Transpose[Table[N[Range[1/h, 1, 1/h]], {w}]]
Formula 4: pattern = Table[N[(1 + Sin[ 2 Pi 1 y/h]*Sin[ Pi 1x/w])/2], {y, h}, {x, w}]
Formula 5: pattern = Table[N[Mod[y, x]], {y, h}, {x, w/4}]
Formula 6: pattern = Table[N[(1 + Cos[ Pi y/h ]*Tan[ Pi x/w])/2], {y, h}, {x, w}]
Formula 7: pattern = Table[Exp[-((4 (x - w/2)/w)^2 + (4 (y - h/4)/(h/a))^2)] + Exp[-((4 (x - w/2)/w)^2 + (4 (y - 3 h/4)/(h/a))^2)], {y, h}, {x, w}]
Formula 8: pattern = Table[N[(1 + Sin[ Pi y/h ]*Tan[ Pi x/w])/2], {y, h}, {x, w}]
Formula 9: pattern = Table[Cos[-((3 (x - w/2)/ w)^2 + (3 (y - h/2)/(h/a))^2)] Exp[-0.05 ((4 (x - w/2)/ w)^2 + (4 (y - h/2)/(h/a))^2)], {y, h}, {x, w}]
Formula 10: pattern = Table[N[(1 + Sin[ 4Pi y/h ]*Tan[ 2 Pi x/w])/2], {y, h}, {x, w}]
Formula 11: pattern = Flatten[{Table[Range[1/w, 1, 1/w], {h/2}], Table[Range[1, 1/w, -1/w], {h/2}]}, 1]
Formula 12: pattern = Table[N[(1 + Sin[ 4Pi y/h ]*Tan[ Pi x/w])/2], {y, h}, {x, w}]
Formula 13: pattern = Table[Exp[-((4 (x - w/2)/w)^2 + (4 (y - h/2)/(h/a))^2)], {y, h}, {x, w}]
Formula 14: pattern = Table[N[Mod[x, y]], {y, h}, {x, w}]
Formula 15: pattern = Table[N[Range[1/w, 1, 1/w]], {h}]
Formula 16: pattern = Table[(x/w + a y/h)/(1 + a), {y, h}, {x, w}]
I think the meaning of the Mathematica functions Range, Table, N, Flatten, Transpose and so on can be easily guessed. If you have problems, send me an email!
back to DMLC home